Ctrl+K

1.1 Continuum Mechanics and Vector Calculus

1.1 Continuum Mechanics and Vector Calculus#

Lecture 1.1
Saskia Goes, s.goes@imperial.ac.uk

Table of Contents#

Primary Learning Materials#

  • Lecture notes in ppt or Jupyter notebook

  • Problem sets and solutions in Jupyter notebook

All content available on GitHub

Introduction#

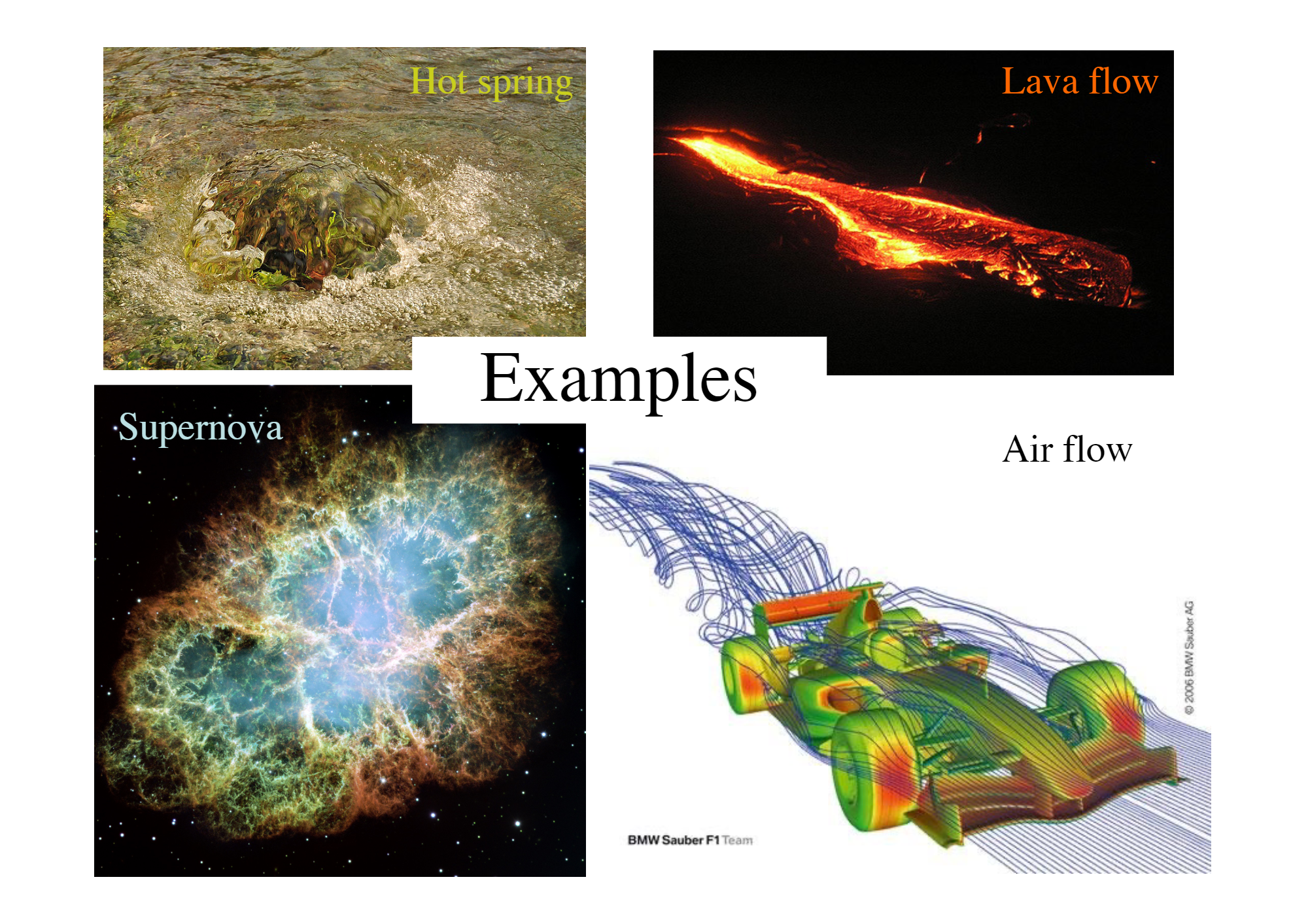
Continuum Mechanics#

  • Macroscopic description of the collective behaviour of atoms/molecules in the limit where scale of interest >> scale of the individual components

  • A material, be it solid, liquid, or gas is treated as a hypothetical continuum where all quantities vary continuously so that spatial derivatives exist -In such a treatment, we can consider infinitesimally small volumes of the material and define point quantities, like mass, velocity, stress -Such a description has been found to be applicable in a wide range of problems in engineering and physical sciences

../_images/Hotspring.png

Continuum Mechanics Equations#

General:

  1. Kinematics – describing deformation and velocity without considering forces

  2. Dynamics – equations that describe force balance, conservation of linear and angular momentum

  3. Thermodynamics – relations temperature, heat flux, stress, entropy

Material Specific:

  1. Constitutive equations - relations describing how material properties vary as a function of T,P, stress, etc. Such material properties govern dynamics (e.g. density), response to stress (viscosity, elastic parameters), heat transport (thermal conductivity, diffusivity)

These equations yield a set of Partial Differential Equations that can be solved for displacement, velocity, temperature, etc…

Differential Equations#

  • Ordinary Differential Equations - describe how variables depend on a single independent parameter (e.g. time or distance). Take Newton’s second law for example,

\[ m\frac{d^2x}{dt^2} = F \]

  • Partial Differential Equations - describe how variables depend on several independent parameters (e.g. time, x,y,z coordinates). For example, the thermal diffusion equation,

\[ \frac{\partial T}{\partial t} = k \frac{\partial ^2 T}{\partial x^2} \]

\(\partial\) - partial derivative

Vectors and Tensors#

Revision topics for vectors

  • Addition, linear independence

  • Orthonormal Cartesian bases, transformation

  • Multiplication

  • Derivatives, del, div, curl

Revision / introductory topics for tensors

  • Tensors, rank, stress tensor

  • Index notation, summation convention

  • Addition, multiplication

  • Tensor calculus: gradient, divergence, curl, ect…

Learning Outcomes #

  1. Be able to perform vector/tensor operations (addition, multiplication) on Cartesian orthonormal bases

  2. Be able to do basic vector/tensor calculus (time and space derivatives, divergence, curl of a vector field) on these bases.

  3. Perform transformation of a vector from one Cartesian basis to another.

  4. Understand differences/commonalities between tensor and vector

  5. Familiarity with index notation and Einstein convention

Introduction to Vectors and Tensors#

Continuum mechanics equations require vectors and tensors, e.g. velocity is a vector, with magnitude and direction in 3-D, and so are forces like gravity. The components of a vector depend on the coordinate system chosen to represent them in. However, the actual size and orientation of the vector is not dependent on the choice of coordinate system

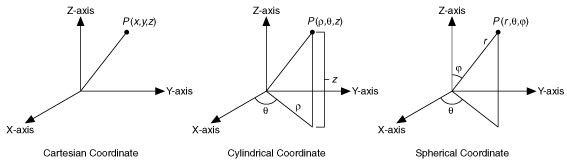
../_images/CoordinateSystems.jpg

note the size and orientation of the vector is the same regardless of coordinate system

Key Characteristics of a Vector#

Which of the following are true of vectors?

  1. Anything that is not a scalar

  2. Has three components

  3. Has magnitude and direction

  4. Depends on coordinate frame

  5. Velocity and rotation are two examples

  6. Multiplication of two vectors gives another vector

Notation#

  • Vectors writen as \(\boldsymbol{v}\), \(\bar{v}\), or \(\overrightarrow{v}\)

  • Length of vectors written as \(v\) or \(\lvert \boldsymbol{v} \rvert\)

  • Vector in Cartesian components written as \(v_x , v_y , v_z\)

  • Index notation, \(v_i\) where \(i = x,y,z\) or \(i = 1,2,3\)

  • Unit vector along direction of \(\boldsymbol{v}\) written as \(\hat{e_v}\)

The unit vector is defined as follows,

\[\hat{e_v} = \frac{\boldsymbol{v}}{\lvert \boldsymbol{v} \rvert}\]

Hence,

\[\boldsymbol{v} = \hat{e_v} \lvert \boldsymbol{v} \rvert\]

Vector properties#

Vectors satisfy certain rules of addition and scalar multiplication

  • \(\mathbf{a} + \mathbf{b} = \mathbf{b} +\mathbf{a}\) (commutative)

  • \((\mathbf{a} + \mathbf{b}) + \mathbf{c} = \mathbf{a} +(\mathbf{b} + \mathbf{c})\) (associative)

  • \(\alpha (\mathbf{a} + \mathbf{b}) = \alpha\mathbf{a} + \alpha\mathbf{b}\) (distributive)

  • \(\mathbf{a} + 0 = \mathbf{a}\) (zero vector)

  • \(1 \cdot{} \mathbf{a} = \mathbf{a} \cdot 1\) and \(0 \cdot{} \mathbf{a} = 0\)

../_images/vector_sum.png

We will see that similar rules apply to tensors. See http://mathworld.wolfram.com/Vector.html for more details

Finite rotation “Vector”#

A finite rotation can be represented as a pseudo-vector. The direction of the vector forms the axis of rotation and the magnitude represents the angle rotated. For the direction of rotation the right hand rule is used where the thumb aligns to the axis of rotation and the fingers point in the direction of rotation.

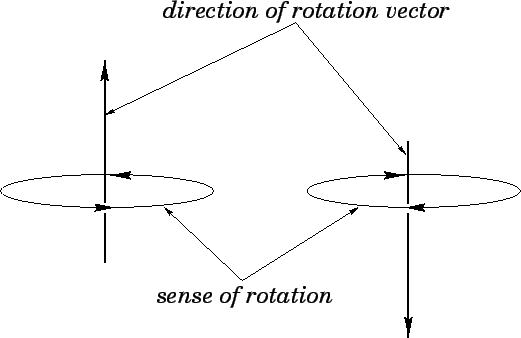
../_images/Rotationvector.png

The reason that finite rotation is a pseudo-vector is that the addition of two finite rotations is not commutative. Hence finite rotations do not satisfy the properties of a vector. However, an infinitesimal rotation is considered a vector.

Linear independence#

Vectors \(\mathbf{v_1}\) through \(\mathbf{v_n}\) are linearly dependent if coefficients \(c_i\) can be found such that:

\(c_1 \mathbf{v_1} + c_2 \mathbf{v_2} + c_3 \mathbf{v_3} + ... + c_n \mathbf{v_n} = 0\) where \(c_i \neq 0\)

Hence, vectors are linearly independent if they cannot be written as linear combinations of each other.

  • Two linearly dependent vectors are parallel/colinear

  • Three linearly dependent vectors are coplanar

  • Four or more vectors are always linearly dependent

Important for defining bases and finding independent solutions to a problem. Practice for this is in Exercise 2

Inner, dot, or scalar product#

\[ \mathbf{F} \cdot \mathbf{d} = \lvert \mathbf{F} \rvert \lvert \mathbf{d} \rvert \cos{\theta} \]

  • Produces a scalar (hence the name scalar product)

  • gives the projection of \(\mathbf{F}\) on \(\mathbf{d}\) scaled by \(\lvert \mathbf{d} \rvert\)

  • \(\mathbf{F} \cdot \mathbf{d} = \mathbf{d} \cdot \mathbf{F}\)

  • \(\mathbf{a} \cdot \mathbf{a} = length(\mathbf{a})^2 = \lvert \mathbf{a} \rvert^2\)

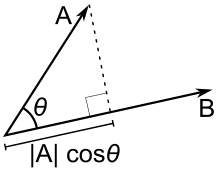
../_images/Dotproduct.png

The scalar product has several physical interpretations. For example, if \(\mathbf{F}\) is force and \(\mathbf{d}\) is displacement, then \(\mathbf{F} \cdot \mathbf{d}\) is the work done by the force \(\mathbf{F}\) for displacement \(\mathbf{d}\)

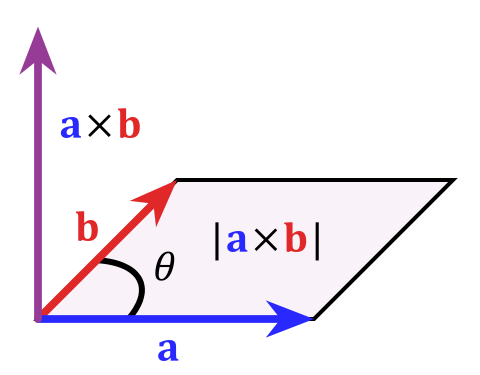
Cross, vector, or outer product#

  • Produces a vector

  • Magnitude of cross product is the area of a parallellogram spanned by \(\mathbf{a}\) and \(\mathbf{b}\)

  • Direction of cross product is normal to the plane of \(\mathbf{a}\) and \(\mathbf{b}\)

  • if \(\mathbf{a}\) and \(\mathbf{b}\) are parallel cross product = 0

  • \(\mathbf{a} \times \mathbf{b} = -\mathbf{a} \times \mathbf{b}\)

../_images/cross_product.png

One physical application of the cross product is in calculating moments. If \(\mathbf{r_{AB}}\) is the moment arm between the pivot point A and the force \(\mathbf{F_B}\), then the resulting moment is calculated as

\[ \mathbf{M_A} = \mathbf{r_{AB}} \times\mathbf{F_B} = aF\sin{\phi} \hat{\mathbf{e_M}} \]
../_images/Moment_cross_product.PNG

Product calculations#

The products of vectors in rectangular Cartesian coordinates:
2D

\[\mathbf{v} \cdot \mathbf{w} = v_1 w_1 + v_2 w_2\]
\[\mathbf{v} \times \mathbf{w} = (v_1 w_2 - v_2 w_1) \hat{\mathbf{e_3}}\]

3D

\[\mathbf{v} \cdot \mathbf{w} = v_1 w_1 + v_2 w_2 + v_3 w_3\]
\[\begin{split}\mathbf{v} \times \mathbf{w} = \left(\begin{array}{cc} v_2 w_3 - v_3 w_2\\ v_3 w_1 - v_1 w_3\\ v_1 w_2 - v_2 w_1\\ \end{array}\right)\end{split}\]

Rectangular Cartesian Coordinate System#

The rectangular Cartesian coordinate system has an orthonormal basis. This means that the basis vectors are all unit vectors, orthogonal to each other.

\[ \hat{\mathbf{e_i}} \cdot \hat{\mathbf{e_j}} = 0 \iff i \neq j \]
\[ \hat{\mathbf{e_i}} \cdot \hat{\mathbf{e_i}} = \lvert \hat{\mathbf{e_i}} \rvert^2 = 1 \]

Cartesian orthonormal bases will be assumed for most of this class

../_images/Other_bases.png

Equivalence of Cartesian geometric and algebraic dot product#

\[ \mathbf{a} = \sum_i a_i \hat{\mathbf{e_i}} \]
\[ \mathbf{b} = \sum_i b_i \hat{\mathbf{e_i}} \]
\[ \mathbf{a} \cdot \hat{\mathbf{e_i}} = \lvert \mathbf{a} \rvert \lvert \hat{\mathbf{e_i}} \rvert \cos{\theta_i} = \lvert \mathbf{a} \rvert \cos{\theta_i} = a_i \]
\[ \mathbf{a} \cdot \mathbf{b} = \mathbf{a} \cdot \sum_i b_i \hat{\mathbf{e_i}} = \sum_i b_i (\mathbf{a} \cdot \hat{\mathbf{e_i}}) = \sum_i b_i a_i = \sum_i a_i b_i \]

Cartesian algebraic cross product#

../_images/cartesian.PNG

Recall that the result of the cross product has a magnitude equal to the area of a parallellogram formed by the two vectors, and has direction normal to the parallellogram. From this it can be seen that \(\hat{\mathbf{e_1}} \times \hat{\mathbf{e_2}} = \hat{\mathbf{e_3}}\). Using the properties of cross product we can also see that \(\hat{\mathbf{e_2}} \times \hat{\mathbf{e_1}} = -\hat{\mathbf{e_3}}\)

Using the basis vectors, the 2D cross product result can be shown fully as:

\[ \mathbf{a} \times \mathbf{b} = (a_1 \hat{\mathbf{e_1}} + a_2 \hat{\mathbf{e_2}}) \times (b_1 \hat{\mathbf{e_1}} + b_2 \hat{\mathbf{e_2}}) \]
\[ = a_1 b_1 (\hat{\mathbf{e_1}} \times \hat{\mathbf{e_1}}) + a_1 b_2 (\hat{\mathbf{e_1}} \times \hat{\mathbf{e_2}}) + a_2 b_1 (\hat{\mathbf{e_2}} \times \hat{\mathbf{e_1}}) + a_2 b_2 (\hat{\mathbf{e_2}} \times \hat{\mathbf{e_2}}) \]
\[ = (a_1 b_2 - a_2 b_1)\hat{\mathbf{e_3}} \]

Triple Products #

  • \(\mathbf{a}(\mathbf{b}\cdot\mathbf{c})\) is a vector multiplied by a scalar

  • \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})\) is the scalar triple product

    • \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c}) =(\mathbf{a}\times\mathbf{b})\cdot\mathbf{c}\)

    • \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c}) = \mathbf{c}\cdot(\mathbf{a}\times\mathbf{b}) = \mathbf{b}\cdot(\mathbf{c}\times\mathbf{a})\) (with cyclical permutation)

    • \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c}) = -\mathbf{a}\cdot(\mathbf{c}\times\mathbf{b}) =-\mathbf{c}\cdot(\mathbf{b}\times\mathbf{a}) = -\mathbf{b}\cdot(\mathbf{a}\times\mathbf{c})\) (with order changed)

    • \(\mathbf{a}\cdot(\mathbf{b}\times\mathbf{c}) = 0 \) if \(\mathbf{a}, \mathbf{b}, \mathbf{c}\) are coplanar

  • \(\mathbf{a} \times (\mathbf{b} \times \mathbf{c})\) lies in plance formed by \(\mathbf{b} \times \mathbf{c}\) normal to \(\mathbf{a}\)
    \( \neq (\mathbf{a} \times \mathbf{b}) \times \mathbf{c}\)
    \( = (\mathbf{a} \cdot \mathbf{c}) \mathbf{b} - (\mathbf{a} \cdot \mathbf{b}) \mathbf{c}\)

See \(\color{blue}{\text{Exercise 8}}\)

Covered so far#

  • Revision of main characteristics of a vector

  • Linear independence of vectors

  • Vector products: dot product, cross product

  • Definition Cartesian orthonormal basis

Take a break, then try yourself#

  • If the material covered so far was all familiar, please skip to \(\color{blue}{\text{Exercise 2}}\) in the notebook

  • If you would benefit from recapping vector products, please look at \(\color{green}{\text{Exercise 1}}\) first

Contents